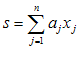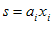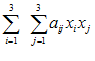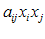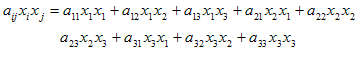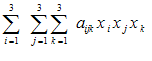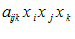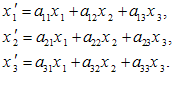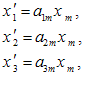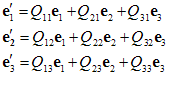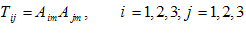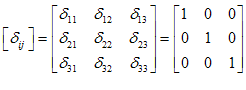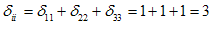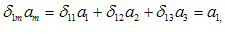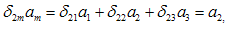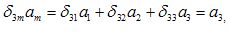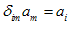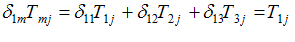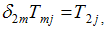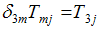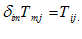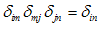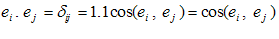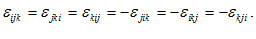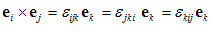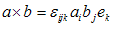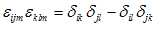نمادگذاری شاخصی

1. مقدمه

نمادگذاری شاخصی كاهش زیادی در جملات یك معادله و رابطه داشته و تاحد زیادی رابطه را عام و یا ساده می كند. بنابراین معمولاً در گزارشها و مقالات اخیر، كه در آنها راجع به تنش، كرنش و معادلات پایه بحث می شود، زیاد بكار می روند. به این لحاظ، یك درك، شناخت و اطلاعات پایه از این نمادها در فرضیه های خمیری، مدل سازی و فرآیندهای شكل دهی فلزات لازم است. با این نمادها، روابط بین تنش و كرنش به شكل خلاصه بیان شده و توجه بیشتر به اصول فیزیكی رابطه و معادله آن می شود.

1. قرارداد جمع، شاخصهای تكراری یا كاذب (dummy index)

جمع زیر را در نظر بگیرید:

1.                         
   

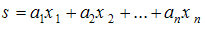
   معادله فوق را می‌توان با استفاده از علامت جمع، به شكل فشرده نوشت:
   

2.                                     
   

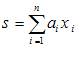
   واضح است كه معادلات زیرین، دقیقاً هم معنای معادله ‏(2-2) می‌باشند:
   

1.                                     

 

•                                         

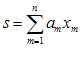
  و غیره.

  شاخص i در معادله ‏(2-2)، یا j در معادله ‏(2-3)، یا m در معادله ‏(2-4) یك شاخص تكراری یا كاذب هسنتد و یكبار در عبارات تكرار شده اند و نتیجه جمع، از حرف به كار برده شده، مستقل است.

  صورت معادله ‏(2-1) را با قرارداد زیر می‌توان بیشتر ساده نمود: هرگاه شاخصی یك بار تكرار شود، یك شاخص تكراری و یا كاذب بوده و مبین جمع روی شاخص با حوزه تغییر اعداد صحیح 1، 2 ، … ، n می‌باشد.
  این قرارداد، به عنوان قرارداد جمع
  انیشتین مشهور است. معادله ‏(2-1) با استفاده از این قرارداد، به صورت زیر خلاصه می‌شود:

  1.                                 
     

  توجه كنید كه:
  

•                             

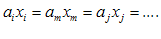
  در این جا بایستی تأكید كرد كه عباراتی نظیر 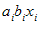در حوزه این قرارداد نمی‌گنجد. یعنی هنگامیكه قرارداد جمع اعمال می‌شود، یك شاخص، هرگز نباید بیش از یك بار تكرار شود. بنابراین، عبارتی نظیر:

  
  
  

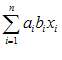
  باید علامت جمع خود را حفظ كند.

  برای آنچه در پیش است، همواره n را برابر 3 انتخاب می شود. به عنوان مثال:
  

  

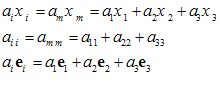
  واضح است كه قرارداد جمع را می‌توان برای نشان دادن یك جمع دوگانه یا سه گانه و غیره به كار گرفت. به عنوان مثال می توان عبارت

  1.                                 
     

  را به صورت ساده زیر نوشت:
  

  1.                                     
     

  بسط كامل عبارت ‏(2-8) ، جمعی با 9 جمله را به دست می‌دهد، یعنی
  

  1.             
     

  احتمالاً برای مبتدیان بهتر آن است كه بسط فوق را در دو مرحله انجام دهند،‌ نخست جمع روی i و سپس جمع روی j (و یا بالعكس). یعنی
  

  
  
  

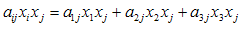
  كه
  

  
  

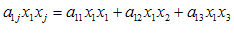
  و غیره.
  

  به طور مشابه جمع سه گانه
  

  1.                     
     

  به سادگی بصورت زیر نوشته می‌شود:
  

  1.                                     
     

  عبارت ‏(2-11) نشانگر یك جمع با 27 جمله است.
  

  مجدداً تأكید می‌شود كه عباراتی نظیر 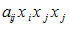یا 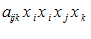در قرارداد جمع، تعریف نمی‌شوند، این عبارات نمایشگر جمعهای زیر نیستند:
  

  
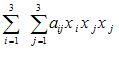      یا     
  

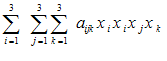
  1. شاخصهای آزاد

  دستگاه سه معادله زیر را در نظر بگیرید:
  

  1.         
     

  با استفاده از قرارداد جمع، معادلات ‏(2-12) را می‌توان به صورت زیرنوشت:
  

  1.                         

 

كه می‌توان آنها را به صورت زیر خلاصه نمود:

 

•                 
  

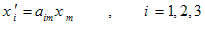
  شاخصی كه تنها یك بار در هر یك از جمله‌های یك معادله – نظیر شاخص i در معادله ‏(2-14) ظاهر می‌شود شاخص آزاد خوانده می‌شود. شاخص آزاد، در هر زمان یكی از اعداد صحیح 1، 2، یا 3 را می‌پذیرد. بنابراین، معادله ‏(2-14) خلاصة سه معادله‌ای است كه هر كدام شامل سه جمله در طرف راست خود می‌باشند[یعنی معادلات ‏(2-12)].
  

  معادله زیر مثال دیگری است:
  

  1.          ,
     

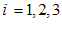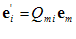
  كه مبین معادلات زیر است:
  

  1.                             

 

توجه شود كه 3 ، 2 ، 1j = ، 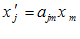نظیر معادله‏(2-14) و 3 ، 2 ، 1j = ، 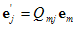نظیر معادله ‏(2-15) می‌باشد. معادله 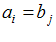بی‌معنا است. شاخص آزاد (كه در تمامی جملات یك معادله ظاهر می‌شود) باید یكسان باشد. بنابراین، معادلات زیر دارای معنی هستند:

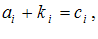
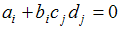
چنانچه در یك معادله، دو شاخص آزاد ظاهر شود ، نظیر

1.                     
   

آن‌گاه، معادله خلاصه شدة 9 عبارت خواهد بود. به عنوان مثال، معادله ‏(2-17) 9 عبارتی را نمایش می‌دهد كه هر كدام دارای سه جمله در طرف راست می‌باشند . در حقیقت :

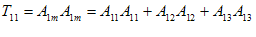
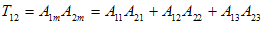
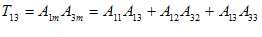
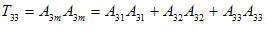
مجدداً معادلاتی نظیر

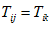
فاقد معنی هستند.

 

 

1. دلتای كرانكر

دلتای كرانكر (كه با 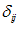نمایش داده می‌شود) به صورت زیر تعریف می‌شود.

1.                 
   

یعنی

                                    

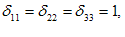
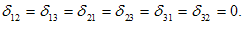
به عبارت دیگر، ماتریس دلتای كرانكر یك ماتریس واحد است. یعنی

1.                 

به موارد زیر توجه شود:

1.                     
   

   
   

   

   

یا به طور كلی

1.                             
   

                   
   

   
   

یا به طور كلی

1.                                     
   

و به خصوص

                                    

1. 
   
   

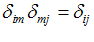
و غیره.

(د) اگر 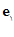، ،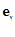 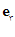بردارهای یكة عمود بر هم باشند، آن گاه

1.         
   

1. نماد جایگشت (تانسور تبدیل)

نماد جایگشت، كه با 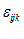(تانسور مرتبهسه) نشان داده می‌شود، به صورت زیر تعریف می‌گردد:

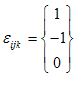
یعنی

                            

                                 

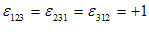
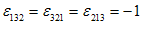
و

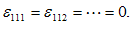
توجه كنید كه

1. 
   

اگر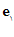، ،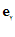 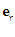یك دستگاه سه عضوی راستگرد را تشكیل دهند ، آن گاه

     e₁´e₂=e₃ ،
e₂´e₃=e₁ ،
e₂´e₁=-e₃، e₁´e₁=0، …

كه می‌توان آن را به صورت زیر خلاصه كرد:

1. 
   

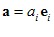حال اگر و 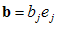باشند، آن گاه

                

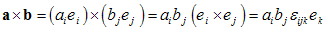
یعنی

1.                         

اتحاد مفید زیر را می‌توان اثبات نمود :

1.                              
   

1. عملیات با نماد گذاری شاخصی

(الف) جایگزینی

اگر

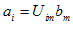                          (i)

        
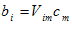
          (ii)

آن گاه برای این كه 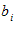ها در (ii) ، را در (i) جایگزین سازیم ، نخست شاخص آزاد عبارت (ii) را از i به m و شاخص كاذب را ازm به حرف دیگری ، مثل n تغییر می‌دهیم ، به طوری كه

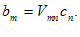                         (iii)

در اینصورت، از (i) و (ii) عبارت زیر حاصل می‌شود

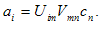                                 (iv)

توجه كنید كه (iv) مبین سه معادله است كه هر كدام شامل 9 جمله در طرف راست خود می‌باشند .

(ب)ضرب

اگر

                              
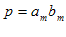
         (i)

و

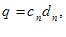                              (ii)

آن‌گاه

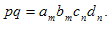                               (iii)

توجه به این نكته مهم است كه 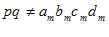. در حقیقت طرف راست عبارت، حتی در قرارداد جمع تعریف نشده است و نیز واضح است كه

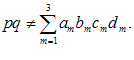
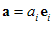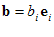چون ضرب داخلی بردارها توزیع‌پذیر است، لذا اگر و باشند، آن گاه

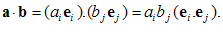                             (iv)

به خصوص اگر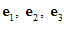 بردارهای یكه عمود بر هم باشند، آن گاه 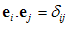به طوری كه

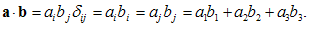                     (v)

(پ) فاكتورگیری

اگر

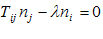                                      (i)

با استفاده از دلتای كرانكر می‌توان نوشت:

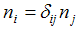                                          (ii)

از این رو (i) چنین می‌شود

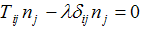                                  (iii)

بنابراین

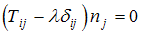                                  (iv)

 

(ت) اختصار یا انقباض

عمل یكسان سازی دو شاخص و سپس جمع‌ آنها را انقباض گویند. هر انقباض دو مرتبه در عبارت كاهش می دهد. به عنوان مثال 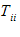انقباض 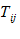می‌باشد:

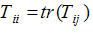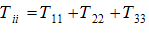                                      (i)

و 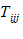انقباض 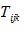است.

اگر

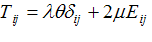                                  (ii)

آنگاه

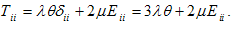                          (iii)

 

———————————————————————